Mathematik kann allerhand: wir berechnen mit ihrer Hilfe, ob am Ende des Monats noch genügend Geld am Konto ist, wie groß die Gewinnchancen beim Roulette sind oder ob die Brücke auch noch nach der Errichtung stehen bleibt und welche Last sie trägt. Sie ist unverzichtbares Werkzeug in der Physik, im Finanzwesen, in der Soziologie und überhaupt. Auch wenn sie sich nur mit sich selbst beschäftigt, liefert sie seit über zwei Jahrtausenden Stoff für knifflige Rätsel und verblüffende Erkenntnisse. Als der deutsche Physiker und Astronom Karl Schwarzschild (1873 - 1916) in seinem letzten Lebensjahr aus Einsteins Allgemeiner Relativitätstheorie (1915) eine exakte Lösung für das Gravitationsfeld einer kugelförmigen, nicht rotierenden Masse ableitete, dachte man auch an eine rein akademische Spielerei. Der Bezug zur Realität (Schwarzes Loch) war weder erkennbar, noch absehbar.
In wie weit Mathematik tatsächlich die Sprache der Natur ist oder sich ihr nur beschreibend annähert, ist - rein wissenschaftlich gesehen - noch nicht geklärt. Ist sie eine Erfindung des Menschen oder ist sie Teil der Natur und liefert daher korrekte Baupläne für Schneckenhaus und Universum? Endgültige Antworten ohne Möglichkeit des Einspruchs bieten nur metaphysische Welterklärungen wie Esoterik, Religion, also jeglicher Art von Mystik (alt und neu) und darauf aufbauende Geheimlehren. TechnoSoph ist an jeglichem Weg zu Erkenntnis und Weisheit interessiert und kennt keine Berührungsängste. In diesem Artikel bleiben wir aber ganz stabil am Boden der Wissenschaft, Mathematik ist und bleibt dabei eines ihrer wichtigsten Hilfsmittel.
Die, nach dem großen italienischen Rechenmeister Leonardo Fibonacci, auch bekannt als Leonardo da Pisa (1170 - 1240) benannte, unendliche Folge Natürlicher Zahlen (ℕ), in der die nächste Zahl immer aus der Summe der beiden Vorgänger gebildet wird, war bereits im Altertum bekannt. Die Inder nutzten die Fibonacci-Folge als Versmaß in den Schriften der Veda, die alten Griechen in Architektur und Kunst. Eine Vielzahl heute noch erhaltener Skulpturen und Bauwerke weisen Proportionen auf, die auf dieser Reihe beruhen. Der Goldene Schnitt (lat., sectio aurea) wurde bereits von Euklid von Alexandria (um 300 vor Chr.) erwähnt, verbreitet hat sich diese Bezeichnung aber erst in der Neuzeit. Proportionen im Verhältnis des Goldenen Schnitts werden vom Menschen als besonders ausgewogen und ästhetisch wahrgenommen. Leonardo Fibonacci sah keine Verwendung dafür, schließlich war er als Rechenmeister an der konkreten Lösung praktischer Probleme interessiert, weniger an Kunst und Architektur. Seine wichtigste Hinterlassenschaft ist jedoch das "Liber Abbaci" ("Buch der Berechnung" oder "Rechenbuch", 1202), das dazu beitrug, die bis dahin gebräuchlichen lateinischen Ziffern (I, V, X, C...) durch die heute verwendeten (indo-arabischen) zu ersetzen. Ein Artikel auf TechnoSoph darüber befindet sich hier.
Wie kam Leonardo Fibonacci auf diese Zahlenfolge?
Die Berechnung von Kaninchenpopulationen war eine der vielen Rechenaufgaben in seinem "Liber Abbaci", anhand derer er die Vorzüge der neuartigen und damals in Europa unbekannten Ziffern fördern wollte.
Ausgangsbedingungen: ein Kaninchenpaar (♂+♀), das nach genau einem Monat Nachwuchs (ein weiteres Paar) bekommt. Dieses ist im ersten Monat noch nicht fortpflanzungsfähig bzw. bekommt erst im 2. Lebensmonat ihrerseits wieder genau ein Paar Kaninchenbabys (also Latenzzeit 1 Monat). Einmal erwachsen, produziert jedes Paar wieder endlos jeden Monat ein weiteres Paar. Es handelt sich um eine idealisierte Rechenaufgabe, daher sterben die pelzigen Nager nicht und werden niemals krank.
Bevor's los geht, hat man natürlich 0 Paare. Man setzt das erste Paar aus: 1. Im darauf folgenden Monat kommt noch kein neues auf die Welt (Latenzzeit 1 Monat): weiterhin 1. Im nächsten Monat haben sie sich endlich vermehrt: 2. Im nächsten Monat produziert das erste wieder ein neues Paar, das zweite ist noch beim... üben: 3. Nächster Monat, die ersten zwei Paare vermehren sich, das dritte ist am... üben: 5. Das geht immer so weiter und wird beim beschreiben und im Kopf mitrechnen immer unübersichtlicher. Man erkennt aber bereits das endlos fortzuführende Muster: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 usw. Am besten, man wechselt zur mathematischen Schreibweise und erstellt eine rekursive (sie greift immer auf's vorhergehende Resultat zurück) Funktion:

Wie komme ich damit zum Golden Schnitt?
Aus der oben berechneten Anzahl an Kaninchenpaaren jeden Monats erhalten wir die Folge: 0, 1, 1, 2, 3 , 5, 8, 13, 21, 34, 55, 89 usw. Dividiert man nun eine der Zahlen durch ihren Vorgänger nähert man sich immer weiter der irrationalen Zahl Φ ≈ 1,6180339887... an - am Beginn noch arg daneben, pendelt das Ergebnis (mal oberhalb, mal unterhalb) immer näher Richtung Φ (griech., Phi). Das ist das gebräuchlichen Zeichen für den Goldenen Schnitt oder klein geschrieben φ.
Die herkömmliche - und in der Mathematik bevorzugte - Methode Φ zu berechnen ist allerdings durch Stetige Teilung (alternative, aber seltene Bezeichnung für den Goldenen Schnitt) einer Strecke a+b in zwei Teilstrecken a und b, so dass sich die längere Teilstrecke a zur kürzeren b verhält wie die Summe der beiden a+b zu a. Das gelingt ausschließlich, wenn das Verhältnis von a:b 1:1,6180339887... ergibt.
Es gilt: a ist die längere Teilstrecke, b die kürzere
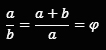
Lösung der Gleichung:
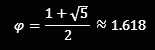
Der Goldene Schnitt hat nicht nur in der Geometrie Bedeutung, er kann auch algebraisch als die positive Lösung der quadratischen Gleichung
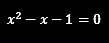
definiert werden. Details zur Lösung beider Gleichungen erscheinen zu einem späteren Zeitpunkt in einem ausführlicheren Artikel, der sich ausschließlich dem Goldenen Schnitt und seinen besonderen Eigenschaften widmen wird. Von seiner Bedeutung in Kunst, Architektur und der Anwendung der Fibonacci-Folge haben wir bereits erfahren, bleibt noch das letzte und größte Rätsel:
Wie kommen beide in die Baupläne des größten aller Baumeister, der Evolution?
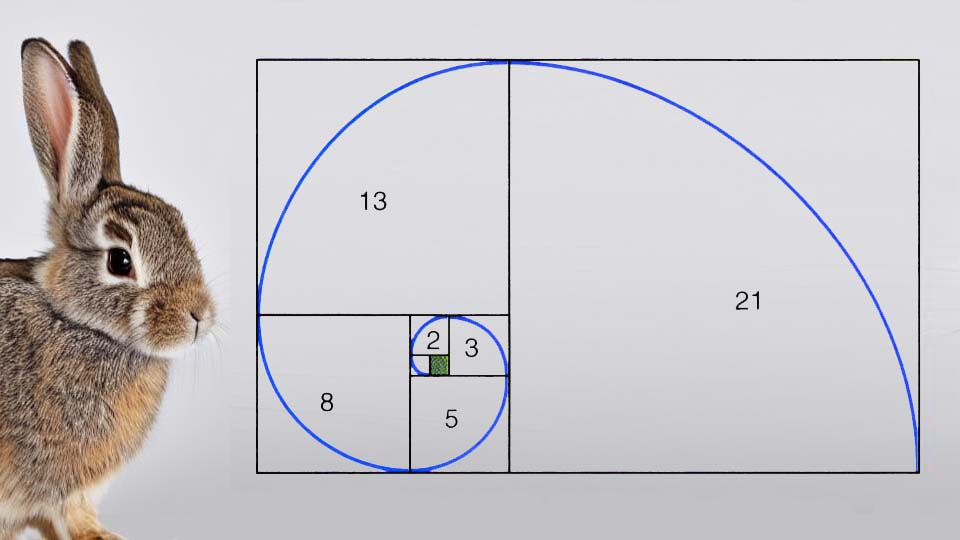
Dazu sehen wir uns zuerst das Titelbild noch einmal genauer an: im Zentrum der Spirale befinden sich zwei Quadrate (das erste grün) mit der Seitenlänge l = 1, darüber eines mit der Seitenlänge l = 2, daneben eines mit Seitenlänge l = 3, darunter eines mit Seitenlänge l = 5, wieder daneben eines mit Seitenlänge l = 8 usw. Sind die Quadrate (das ganze darf auch gerne bis 10946 oder höher fortgesetzt werden...) gezeichnet, wird mit eingeschriebenen Viertelkreisen die sogenannte Goldene Spirale eingezeichnet. Diese ist nicht nur hübsch anzusehen, sondern bildet die geometrische Grundlage zur Konstruktion von Schneckenhäusern, verschiedenen Muscheln und Korallen, Elefantenohren, Sonnenblumen, Rosen, Wirbelstürmen, Spiralgalaxien etc.
Aber nicht nur die Form dieser Spirale taucht in der Natur auf. Mindestens genauso erstaunlich ist die Anzahl der Kerne in der Sonnenblume: meist 34, 55 oder 89 Kerne, Lilien haben 3 Blütenblätter, Butterblumen 5, Gänseblümchen 21 - stets Zahlen aus der Fibonacci-Folge. Ebenso die Anzahl der Vorfahren der männlichen Honigbiene (Drohne), der Türmchen am Brokkoli, die Anzahl der Spiralen in einem Tannenzapfen und auch die Schuppen der Ananas winden sich in Fibonacci-Spiralen um die schmackhafte Frucht.
Die Liste ließe sich beliebig fortführen, nicht nur auf unserem Planeten. So wie's aussieht, ist das Weltall in jeder Hinsicht isotrop. Es sieht nicht nur in jeder Richtung gleich aus, es gilt auch überall die selbe Physik und Mathematik. Die Fibonacci-Folge und der Goldene Schnitt könnten daher wirklich überall zu finden sein, die Wirbelstürme auf Jupiter sind schon mal ein gutes Zeichen in Richtung dieses Gedankens. Die Antwort, warum in der Natur gerade diese Zahlen und Anordnungen zu finden sind, ist weniger göttlich, denn banal: sie bieten einen evolutionären Vorteil. Diese Zahlen und Proportionen ermöglichen eine optimale Ausnutzung des verfügbaren Raums für Blüten um die maximale Menge an Licht einzufangen und für das Wachstum von Korallen oder Schneckenhäusern, die männlichen Bienen (Drohnen) folgen einem ähnlichen Fortpflanzungsmechanismus wie Fibonaccis idealisierte Kaninchen (beziehungsweise die Bienenköniginnen) usw.
Die Frage, ob der Mensch mit der Mathematik ein Werkzeug zur Beschreibung der Natur geschaffen hat oder sie seit je her den grundlegenden Bauplan von allem bildet, stellt sich TechnoSoph gar nicht. Schließlich ist der Mensch genauso Teil der Natur und ohne sie gar nicht denkbar. So wie alles, was er erfindet oder einfach nur entdeckt, bleibt er in einem unaufhörlichen Wechselspiel immer ein Teil davon. So betrachtet bilden auch Technik und Natur keinen Widerspruch und sind ein und dasselbe. Wer die Natur wirklich liebt, liebt daher auch die Mathematik.
„Die Schönheit der Welt ist durch Zahlen geordnet, und der Goldene Schnitt ist eine der tiefsten Harmonien der Natur.“ Verfasser unbekannt