Entropie kann umgangssprachlich auch als Maß für Unordnung gesehen werden. Der fallende Teller, der in Scherben zerbricht, besitzt ein geringeres Maß an Ordnung als das intakte Gefäß davor und auch mit zusätzlichem Aufwand (Kleben) wird er nie mehr das, was er einmal war. Um den Küchenboden wieder in den Zustand der gewohnten Ordnung zu versetzen braucht es Arbeit - also den Einsatz von Energie - und die Information, wo denn alles seinen angestammten Platz hat.
Entropie kann auch nicht vernichtet werden. Selbst ein Prozess, der rückgängig gemacht werden kann, erzeugt ein Mehr an Entropie in der Umgebung des Systems. Der Teller kann zwar mit Klebstoff und etwas Kraftaufwand wieder (ungefähr) in seine ursprüngliche Form gebracht werden, das braucht aber trotzdem Ressourcen, Energie und Information. So wird Entropie auch zum Wegweiser, der die Richtung des Zeitpfeils anzeigt: immer in Richtung zunehmender Entropie.
Allerdings handelt es sich dabei nur um einen bildhaften Vergleich. Entropie beschreibt in der Physik Zustandswahrscheinlichkeiten in geschlossenen thermodynamischen Systemen. Begriffe wie "Ordnung" oder "Unordnung" gibt es hier nicht und der Teller zerbricht nicht (ausschließlich) deshalb, weil sich Teilchen ihrer Temperatur entsprechend frei bewegen können.
Bleiben wir zum besseren Verständnis dennoch kurz bei der umgangssprachlichen Ordnung. Diese wäre in einem perfekten Kristall bei einer Temperatur von null Kelvin theoretisch am höchsten - die Entropie also gleich null. In der Realität existieren aber weder vollkommen perfekte Kristalle (irgendwas erzeugt immer Defekte), noch ist der absolute Nullpunkt von 0 Kelvin (-273,15 Grad Celsius) jemals erreichbar.
Die Abweichung der Verteilung der Teilchen von dieser in der Praxis nicht erreichbaren Ordnung, wird in Entropie angegeben. Nach Rudolf Clausius (1822-1888) beträgt die Entropieänderung
ΔS = Q/T
S steht für Entropie und wird in Joule durch Kelvin angegeben.
Soweit die Definition in der klassischen Thermodynamik. In ihr kann ein System mit seiner Umgebung Energie auf zwei Arten austauschen: in Form von Wärme oder durch die Verrichtung von Arbeit.
Einen etwas anderen Ansatz zur Bestimmung der Entropie verfolgt die statistische Mechanik, in der das Verhalten makroskopischer Systeme durch das mikroskopische Verhalten seiner Komponenten - Atome und Moleküle - erklärt wird. Ihr Begründer James Maxwell (1831-1879) veröffentlichte dazu 1871 ein anschauliches Gedankenexperiment, mit dem Theoretiker sich bis heute die Zeit vertreiben: der Maxwellsche Dämon.
Maxwells Dämon
Man nehme einen zweigeteilten Behälter, in der die Luftmoleküle einer Hälfte durch eine verschließbare Klappe von denen der anderen Hälfte getrennt werden können. Zu Beginn herrscht in beiden Hälften die gleiche Temperatur, die nichts über die Energie (Geschwindigkeit) eines einzelnen Teilchens eines Systems aussagt, sondern stets nur einen Mittelwert darstellt.
Dann beginnt jemand (der "Dämon"), der die Geschwindigkeit jedes einzelnen Luftmoleküls kennt, die Klappe so zu öffnen und wieder zu verschließen, dass am Ende alle Moleküle mit hoher Geschwindigkeit in einer Hälfte gefangen sind und in der anderen Hälfte alle mit niedriger Geschwindigkeit. Die Gesamttemperatur des Behälters bleibt dabei dieselbe, aber eine Hälfte wird dabei immer wärmer und eine immer kälter.
Hätte man einen idealen Verschlussmechanismus (der nur in der Theorie existiert), bräuchte man keine Arbeit beim Öffnen und Schließen der Klappe aufwenden. Damit könnte man eine Wärmekraftmaschine betreiben, die durch die entstandene Temperaturdifferenz selbst Arbeit verrichten könnte. Das ergibt ein Perpetuum mobile und widerspricht dem 2.Hauptsatz der Thermodynamik (siehe hier) und ist daher nicht realisierbar.
Dieses Gedankenexperiment veranschaulicht die Unumkehrbarkeit der Entropie ohne erneuten Einsatz von Energie und Information. Es beinhaltet auch zwei Ausgangsbedingungen, von denen wir wissen, dass sie völlig unrealistisch sind: weder gibt es Gerätschaften, die Arbeit ganz ohne Energieeinsatz verrichten können, noch gibt es "Dämonen", die in der mikroskopischen Welt (Moleküle, Atome und noch kleiner) gleichzeitig etwas über Energiegehalt und Ort eines Teilchens wissen können oder durch die Messung das Ergebnis nicht mit beeinflussen würden. Dieser Umstand war zu Maxwells Lebzeiten noch unbekannt.
Ludwig Boltzmann (1844-1906) wählt für die Bestimmung des Absolutwertes der Entropie auch einen statistischen Zugang. Er verknüpft Entropie mit der Anzahl möglicher Mikrozustände eines makroskopischen Systems:
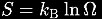
Entropie ist gleich Boltzmann-Konstante (Umrechnungsfaktor von absoluter Temperatur in Energie) mal Zustandssumme (aller enthaltener Teilchen).
Information
Die Erkenntnis, dass Entropie auch mit Information in Zusammenhang stehen muss, verdanken wir Leó Szilárd (1898-1964). Der spätere Mitarbeiter im Manhatten-Projekt lieferte 1929 in seiner Habilitationsarbeit "Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen" eine der Grundlagen für die Informationstheorie, einer mathematischen Theorie aus den Bereichen Wahrscheinlichkeitstheorie und Statistik.
Diese in den 40er und 50er Jahren des 20.Jahrhunderts entstandene Theorie - als ihr Begründer gilt Claude Shannon (1916-2001) - beschäftigt sich mit dem Informationsgehalt (der Informationsdichte) von Nachrichten und kommt außer in der Informatik auch in Bereichen wie Neurologie, Molekularbiologie und Publizistik zur Anwendung.
Szilárds Gedankenexperiment ist eine Weiterentwicklung des Maxwellschen Dämons und reduziert dessen (theoretischen) Versuchsaufbau auf ein einzelnes Molekül in einem zweigeteilten reibungslosen Kolben. Das Molekül nimmt dabei Wärme aus der Umgebung auf - die Temperatur bleibt dabei konstant - und verrichtet Arbeit an einer Masse.
Die einzige Tätigkeit des Dämons bleibt die Messung und da die Temperatur gleich bleibt, muss der Zugewinn an Entropie irgendwo im - durch die Messung gewonnenen - Informationsgehalt oder der Messung selbst beinhaltet sein.
Léon Brillouin (1889-1969) definierte 1951 Information als negative Entropie (Negentropie) und sah in der Messung (durch Photonen) selbst eingeschriebene Information. Anhand indirekter Messungen, quantenmechanischer Methoden oder informationstheoretischer Modelle kann diese Beeinflussung jedoch minimiert und "herausgerechnet" werden.
Die Diskussion des Begriffs Entropie und was es tatsächlich mit ihr auf sich hat, ist noch lange nicht zu Ende. Der Informationstheoretiker Rolf Landauer brachte 1961 die Komponente des Löschens der Information und das damit verbundene Zurücksetzen des Speichers ins Spiel: dabei wird Entropie freigesetzt - im Gegensatz zum Schreiben und Auslesen des Informationsspeichers, die keine Entropieänderung zur Folge haben.
Charles Bennett konnte 1982 durch Anwendung des Prinzips von Landauer zeigen, wie danach das "Gedächtnis" des Maxwellschen Dämons wieder Entropie ins Luftgemisch einbringt um den 2.Hauptsatz zu erfüllen. Orly R. Shenker findet im Jahr 2000 Fehler in der Argumentation Landauers, Oliver Penrose sieht bereits 1970 ohne Kenntnis des Landauer-Prinzips das Zurücksetzen des Speichers als Ursache für eine Verringerung der möglichen Gesamtzustände des Maxwellschen Systems.
Die heutigen Forschungsrichtungen zur Entropie erstrecken sich von der Kosmologie und Schwarzen Löchern ("Hawking-Strahlung") über Quantengravitation ("Quantenrelative Entropie") bis zur Nachhaltigkeit und Klimaforschung ("Prigogine" oder "Nicht-Gleichgewichts-Thermodynamik"). Entropie ist mittlerweile nicht nur ein Begriff der Thermodynamik, sondern auch für Information, Wahrscheinlichkeit und möglicherweise für die Richtung der Zeit.
Auch in den Sozialwissenschaften verwendet man mittlerweile den Begriff Entropie, um Zu- und Umstände sozialer Ungleichheit zu beschreiben. So wie ein physikalisches System mit zunehmender Entropie seine Struktur verliert (schmelzendes Eis), kann auch ein soziales System durch mangelnde Kommunikation, Orientierungslosigkeit oder Werteverfall in einen Zustand der "sozialen Entropie" übergehen.
Man kann nur hoffen, dass unserem sozialen Gefüge nicht dasselbe Schicksal blüht wie - wenn es nach einer der unzähligen Theorien der Astrophysiker geht - unserem Universum: "Big Freeze" oder der Wärmetod. Der tritt aber beruhigenderweise erst in einer Gogol Jahren ein, also in 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 Milliarden Jahren.
Widersprüchlicher Ausblick: der höchste Grad an Entropie - die perfekte Unordnung - bedeutet zugleich ein Maximum an Homogenität und Gleichförmigkeit und ist damit wiederum ein äußerst geordneter Zustand... zumindest aus philosophischer Perspektive, nicht aus der Sicht des Physikers.


