Primzahlen sind lustig: lassen sich nur durch die 1 oder durch sich selbst teilen und je höher die Zahlen, desto seltener tauchen sie auf. Das tun sie dann aber doch immer, ohne Ende. Die höchste bisher entdeckte Primzahl fand der kalifornische Hobbymathematiker Luke Durant im Jahr 2024: sie hat 41.024.320 Stellen und ist das Ergebnis aus 2¹³⁶²⁷⁹⁸⁴¹ -1. Die Beschäftigung mit Primzahlen und ihre besondere Stellung im Reich der Zahlen lässt sich über Jahrtausende zurückverfolgen. Während sie in vedischen Schriften in Indien (dazu: Was ist 'Vedische Mathematik'?) als Versmaß oder in der vedischen Architektur auftauchen, begann im alten Griechenland ab dem 6. vorchristlichen Jahrhundert die - im heutigen Sinne - systematische Untersuchung der Zahlenwelt. Die Primzahlen nahmen einen besonderen Platz ein, wahrscheinlich teilte man damals gern.
Beginnen wir mit der ersten der natürlichen Zahlen, der Zahl 1: sie galt im alten Griechenland nicht als richtige Zahl, diese begannen erst mit der 2. Zahlen wurden als Mengen oder Anzahl von Dingen verstanden, die 1 stand für Einheit und war keine Menge. Bis heute betrachten wir die Menge an Zahlen, die prim sind, erst ab Zahlen größer als 1.
Bereits die Pythagoräer (Anhänger des Pythagoras, 5. und 4. Jhdt v.Chr.) untersuchten Primzahlen im Zusammenhang mit Musiktheorie und Zahlenverhältnissen. Davon unabhängig ging der Mathematiker, Astronom und Philosoph Eratosthenes von Kyrene (~276-194 v. Chr.) nicht nur als Leiter der berühmten Bibliothek von Alexandria in die Geschichte ein und weil er bereits den Erdumfang ebenso korrekt (mit nur 1% Abweichung) berechnete wie die Ekliptik (Neigung der Erdachse), sondern ihm verdanken wir auch das 'Sieb des Eratosthenes', mit dessen Hilfe man aus einer Liste mit ansteigend angeführten Zahlen alle Primzahlen findet, die darin enthalten sind. Dieser Algorithmus existierte bereits vor seiner Zeit, aber Eratosthenes gab ihm den praktischen Namen 'Sieb'.
Sieb des Eratosthenes
Das Verfahren ist recht einfach: man schreibt bei 2 beginnend den gewünschten Zahlenbereich an (zb. 2,3,4,5 bis 100). Zuerst werden alle Zahlen, die ein Vielfaches von 2 sind, durchgestrichen. Es genügt dann beim Streichen der folgenden Vielfachen mit dem Quadrat der Primzahl zu beginnen, da alle kleineren Vielfachen bereits markiert sind. Die kleinste unmarkierte Zahl ab der 2 ist immer eine Primzahl, also ist die 3 eine Primzahl. Nun werden alle Vielfachen von 3 gebildet und gestrichen. Die nächste nicht gestrichene Zahl ist die 5 - also wieder eine Primzahl. Man streicht daraufhin alle Vielfachen von 5. Die nächste verbliebene Zahl ist 7, also wieder eine Primzahl. Dann Streichen aller Vielfachen von 7 und wir haben 11 als nächste noch nicht Gestrichene (und daher: Primzahl). Da mindestens ein Primfaktor einer zusammengesetzten Zahl immer kleiner gleich der Wurzel der Zahl sein muss, ist es ausreichend nur die Vielfachen jener Primzahlen zu streichen, deren Quadrat kleiner als die höchste Zahl des untersuchten Bereichs ist. Da das Quadrat von 11 (11x11=121) bereits außerhalb unseres zu untersuchenden Bereichs liegt, ist das Werk vollbracht: alle noch verbliebenen Zahlen sind prim.
Satz des Euklid
Die Sache mit der 1 hielt auch der große Mathematiker Euklid (3.Jhdt v.Chr.) noch so. Ihm verdanken wir den ersten bekannten formal bewiesenen Satz über Primzahlen und dieser gilt bis heute als grundlegender Lehrsatz der elementaren Zahlentheorie. Nach dem Satz von Euklid steht fest: die Menge der Primzahlen ist unendlich.
In der Antike war das Konzept Unendlichkeit noch nicht bekannt, Euklid formulierte daher: „Es gibt mehr Primzahlen als jede vorgelegte Anzahl von Primzahlen.“
Weiters definiert der Satz von Euklid: eine Primzahl ist eine ganze Zahl größer als 1, die nur durch 1 und sich selbst teilbar ist. Die Liste dieser Zahlen (2,3,5,7,11,13,17...) endet ebenso wenig wie die aller natürlichen Zahlen (1,2,3,4,5,6,7...). Sein vollständiger Beweis dazu ist bis heute im Original erhalten und beschreibt das Verhältnis von (ganzen) Zahlen anhand ihrer dem Wert entsprechenden Längen.
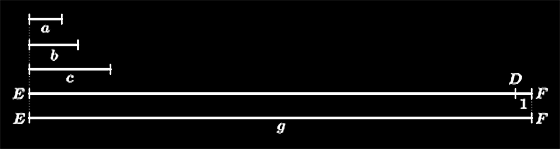
"Die vorgelegten Primzahlen seien a, b, c. Ich behaupte, dass es mehr Primzahlen gibt als a, b, c." Die Erklärung der Abbildung und der vollständige Text von Euklid (hier als PDF in deutscher Übersetzung von Johann Friedrich Lorenz, 1781) vereinfacht wiedergegeben: Euklid verwendet für seinen Beweis die Längen mit dem Betrag dreier Primzahlen (zb. a=2, b=3, c=5) und erzeugt daraus eine neue Strecke DE, indem er zum Produkt der Längen a,b,c 1 addiert. Diese neue Länge g oder Strecke EF [zb. (2x3x5)+1=31] ist immer eine Primzahl. Sie ist durch keine der Ausgangslängen "messbar", wie Euklid formuliert.
Satz von Euler
Die Liste derer, die sich weltweit mit Primzahlen beschäftigten, ist lang und wird immer länger. Dieser Artikel ist nur als ein Einführender gedacht, aber um den kurzen historischen Reigen abzuschließen, sei noch ein Lehrsatz von Leonhard Euler (CH, 1707-1781) erwähnt, der auch mit Beiträgen zur Zahlentheorie Geschichte schrieb. Dieser besagt:
Sei![]()
die Folge aller Primzahlen. Für die Summe aller Kehrwerte gilt:
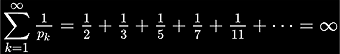
Größenordnung der Partialsummen:
![]()
„Die Summe der reziproken Reihe der Primzahlen
ist unendlich groß, dennoch unendlich mal kleiner als die Summe der harmonischen Reihe
![]()
Und die Summe jener ist quasi der Logarithmus dieser Summe.“
Für Euler war dies ein Indikator, dass die Primzahlen wesentlich dichter liegen als die Quadratzahlen. Er hatte bereits zuvor bewiesen, dass die unendliche Summe der Kehrwerte aller Quadratzahlen gegen einen endlichen Grenzwert strebt. Ob das tatsächlich so ist, ist nach wie vor unklar. Man weiß noch nicht einmal, ob zwischen zwei benachbarten Quadratzahlen stets eine Primzahl liegt (Legendresche Vermutung).
Egal ob im alten China mit ihrer Hilfe Kalenderberechnungen durchgeführt wurden, sie weltweit in der Zahlensymbolik auftauchen oder im mittelalterlichen Orient der große arabische Mathematiker und Geograph Al-Khwarizmi (780-835/850, voller Name: Abū Ǧaʿfar Muḥammad bin Mūsā al-Ḫwārizmī) ihnen seine Zeit widmete, sie nahmen stets einen besonderen Platz in der Welt der Zahlen ein. Ist ja auch kein Wunder, schließlich sind aus ihnen alle anderen zusammengesetzt - jeder kennt die Zerlegung von Zahlen in ihre Primfaktoren. Aber auch in der Natur sind zb. die Fortpflanzungszyklen von Fressfeind und Beute oft in Intervallen aus Primzahlen zu einander versetzt. So begünstigt die Evolution die Vermehrung von manchen Insektenarten, ohne dass sich diese Intervalle mit möglichen starken Jahren ihrer Jäger überschneidet. Die Natur ist prim und erst recht unsere moderne digitale Welt: Primzahlen bilden die Grundlage heute verwendeter (RSA-)Verschlüsselung, der Spektralanalyse oder beim Erzeugen von Zufallszahlen. Generationen von Zahlentheoretikern wird sie noch lange eine ausladende Spielwiese bieten. Auch TechnoSoph wird in kommenden Artikeln noch tiefer in dieses spannende Gebiet eintauchen und wir untersuchen dann genauer, was das alles mit Unendlichkeit oder den langsam aufkommenden Quantenrechnern zu tun hat.


