Vedische Geometrie ist schriftlich belegt und wird heute noch verwendet. Man errichtet mit ihrer Hilfe Altäre, Tempel, konstruiert damit geometrische Muster und führt Berechnungen von Kreisflächen und Durchmessern aus. Darüber hinaus dient sie zur Transformation von Flächen und zur Berechnung von Diagonalen des Rechtecks (entsprechend des Satzes von Pythagoras).
Gearbeitet wird mit Schnüren und Seilen (Rajju, Sulba), die an Fixpunkten in Form von Pfosten oder Stiften (Sanku) gespannt werden. Es ist verblüffend wie so mit einfachsten Mitteln zum Beispiel ein Kreis in ein flächengleiches Quadrat überführt wird. Dazu wird an einem Pfosten im Mittelpunkt ein Seil befestigt und damit ein Kreis in den Sand (auf's Papier) gezeichnet wird. Durch gezieltes Umstecken des Ankerpunktes des Seils ensteht so ein Quadrat mit derselben Fläche.
Sehenswert sind auch die, auf diese Weise generierten, Mandalas - geometrische Schaubilder mit spiritueller und meditativer Bedeutung. Die Anleitungen dazu sind in den Sulbasutras niedergeschrieben und stammen aus der Mitte des ersten Jahrtausends v. Chr.
Der Begriff Vedische Mathematik ist in akademischen Kreisen aber strittig. Konkrete Aufzeichnungen mit Rechenregeln sind nicht erhalten. Die Muster von langen und kurzen Silben in vedischen Sanskrit-Versen folgen aber bereits der viel später als solche bezeichneten Fibonacci-Folge (ein Artikel dazu hier) und deuten daraufhin, dass in Indien Mathematik bereits im Altertum eine bedeutende Rolle spielte.
Das Buch "Vedic Mathematics" (hier im PDF-Format) hingegen stammt von Seiner Heiligkeit Swami Bharati Krishna Tirtha (1884 - 1960) und erscheint posthum 1965. Es bringt die Vedische Mathematik wieder zurück ins Bewusstsein der Menschheit oder ist bestenfalls eine Erfindung des Autors. Je nachdem, woran man glaubt. Der gläubige Hindu sagt so, der aufgeklärte atheistische Rationalist sagt was anderes.
Laut Seiner Heiligkeit wurde sie durch tiefe Meditation in den Wäldern in der Nähe des Klosters Sringeri Math (auch bekannt als Sringeri Sharada Peetham) in Sringeri (Karnataka) empfangen und stammt aus einem verloren gegangenen Anhang des Atharvaveda (Sammlung von Hymnen und Zauberformeln). Belege dafür oder Textfragmente der ursprünglichen Schriften fehlen leider. Erstaunlich praktisch sind die Rechenregeln trotzdem. Da Geometrie ein Teilgebiet der Mathematik ist, existieren daher sowohl Vedische Geometrie als auch Vedische Mathematik.
"Vedische Mathematik"
"Vedic Mathematics" ist eine Sammlung aus 16 Sutras und 14 Sub-Sutras (heilige Aphorismen). Diese Rechenregeln weisen Ähnlichkeiten mit der Trachtenberg-Schnellrechenmethode (nach Jakow Trachtenberg, 1888 - 1951, D) auf, beschleunigen einige arithmetische Rechnungen und erleichtern das Kopfrechnen. Es folgt das Inhaltsverzeichnis und exemplarisch zwei einfache, anschauliche Tricks aus "Vedic Mathematics" und weiter unten tauchen wir mit der Biografie dieses bedeutenden indischen Gelehrten vorsichtig weiter den großen Zeh in den Ozean Östlicher Philosophie und indischer Mystik.
16 Sutras:
- Eins mehr als der davor
- Alle von 9 und die letzte von 10
- Vertikal und kreuzweise
- Stelle um und wende an
- Wenn die Kombination dieselbe ist, ist es Null
- Ist das eine das Verhältnis, ist das andere Null
- Bei Addition und bei Subtraktion
- Bei der Vervollständigung oder Unvervollständigung
- Unterschiedliches Differential- und Integralrechnen
- Bei Unvollständigkeit
- Spezifisch und allgemein
- Die Verbliebene zur letzten Stelle
- Das Letzte und zweimal der Vorletzte
- Einer weniger als der davor
- Das Produkt der Summe
- Alle Multiplikatoren
14 Sub-Sutras:
- Proportionalität
- Die Verbleibende bleibt konstant
- Die Erste zur Ersten und die Letzte zur Letzten
- Der Multiplikant von 7 ist 143
- Bei Berührung
- Ziehe die Differenz ab
- Was immer der Abstand ist, vergrößere den Abstand ein weiteres Mal und stelle das Quadrat des Abstandes her
- Summiere das Letzte mit 10
- Nur die Letzten
- Die Summe des Produkts
- Alternativ mit Ausschluss und Beibehaltung
- Bei bloßer Beobachtung
- Das Produkt der Summe ist die Summe des Produkts
- Mit dem Symbol
Zwei Beispiele daraus:
Das Sutra "Einer mehr als davor" vereinfacht die Multiplikation zweistelliger Zahlen, wenn die ersten Ziffern gleich sind und die hinteren zusammen 10 ergeben. Dabei multipliziert man die erste Ziffer mit ihrem Nachfolger und bekommt die ersten beiden Ziffern des Ergebnisses. Anschließend multipliziert man die beiden zweiten Ziffern unserer Zahl. Das ergibt dann die hinteren beiden Ziffern des Ergebnisses:
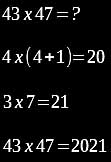
Sutra "vertikal und kreuzweise" vereinfacht die Addition und Subtraktion von Brüchen, indem kein gemeinsamer Nenner gebildet wird, sondern kreuzweise Zähler und Nenner miteinander multipliziert werden:
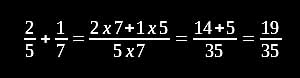
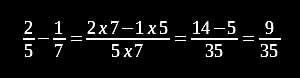
Biographie
Der Verfasser dieser Regeln, Jagadguru Śaṅkarācārya Svāmī Bhāratīkṛṣṇa Tīrtha, war eine beeindruckende Persönlichkeit: er lebte von 1884 - 1960 in Indien und wurde am 14. März in Tirunelveli (im Bundesstaat Tamil Nadu) in eine tamilische Brahmanenfamilie als Venkataraman Shastri hinein inkarniert. Reinkarnation ist im Hinduismus unumgänglich. Atman (die Seele) ist unsterblich und wechselt nach dem Tod von einem Körper zum nächsten. Nur große spirituelle Meister oder Heilige können bewußt über ihre Wiedergeburt entscheiden und sich unter Umständen auch mehrfach gleichzeitig neu manifestieren. Unter welchen Umständen reinkarniert wird, entscheidet das Karma. Schlechte Handlungen wirken sich bei den Hindus wie im Buddhismus ungünstig auf die Wiedergeburt aus.
Brahmanen bildeten die oberste Kaste im traditionellen indischen Kastenwesen. Sie waren ursprünglich Priester und Gelehrte. Die anderen Kasten bildeten die Kshatriyas (Krieger und Herrscher), Vaishyas (Händler und Bauern) und Shudras (Dienende), die Dalits (Unberührbare) standen außerhalb des Kastensystems. Für sie gibt es mittlerweile im modernen Indien Förderprogramme, die schlechte Behandlung und Ungerechtigkeiten beseitigen sollen.
Das Kastenwesen gilt seit der Verfassung des neu gegründeten modernen Indien 1949 als offiziell abgeschafft. Seit der Verfassung von 1950 ist die Diskriminierung ausdrücklich untersagt und steht unter Strafe. Die hinduistische Einteilung in Kasten ist dabei dem Klassensystem in westlichen kapitalistischen Gesellschaften (im Sinne von Karl Marx) nicht unähnlich. Ob und in welcher Form diese Systeme noch immer existieren, darüber scheiden sich hier wie dort die Geister.
Venkataraman Shastri besucht das National College in Trichinopoly und anschließend das Church Missionary Society College in Tirunelveli und besteht 1899 die Zulassungsprüfung der Universität von Madras in Chennai (alle in Tamil Nadu). Dort erhält er ausgezeichnete Noten in Mathematik, Natur - und Geisteswissenschaften inklusive Philosophie, Sprachwissenschaft und Kunstgeschichte.
Seine Vorliebe gilt Sanskrit, eine der ältesten bekannten Sprachen, die zur indogermanischen Sprachfamilie gehört und in der die Veden verfasst wurden. Durch seine Kenntnisse in Sanskrit bekommt er 1899, im Alter von 16 Jahren den Titel "Saraswati". Die hinduistische Göttin des Wissens und der Weisheit, Saraswati, ist Gemahlin Brahmas, des Gottes der Schöpfung und einer der drei hinduistischen Hauptgötter: Brahma, Vishnu und Shiva. Saraswati wird auch oft als Brahmas Shakti (seine weibliche Energie) bezeichnet.
Sein Sanskritlehrer (Guru) war Vedam Venkatrai Shastri, die mündliche Lehre und Überlieferung ist im Hinduismus von großer Bedeutung. 1902 schließt er sein Studium als Jahrgangsbester ab (Bachelor of Arts) und wechselt auf das American College of Sciences in Rochester (New York, USA). In den folgenden Jahren veröffentlicht er Artikel zu den Themen Wissenschaft und Religion und engagiert sich in der "National Education Movement" und gegen die Diskriminierung der Inder in Südafrika.
Seine anschließenden Studien des Hinduismus und im speziellen des Adhyātma-Vidyā (spirituelles Wissen oder Selbsterkenntnis) im Kloster Sringeri Math in Mysore (Karnataka) unterbricht er, unterrichtet drei Jahre lang am National College in Rajamahendry (Andhra Pradesh) und kehrt dann wieder zurück nach Sringeri Math, wo er acht Jahre lang intensiv das Advaita Vedanta (eine der einflußreichsten Richtungen des Hinduismus) und Sastra (die heiligen Schriften der Veden, Brahma-Sutras, Upanishaden und das Bhagavad Gita) unter Jagadguru Sankaracarya Satcitananda Sivabhinava Nrisimha Bharati studiert.
Er praktiziert Brahma-sadhana and Yoga-sādhāna, unterrichtet Sanskrit und Philosophie vor Ort in lokalen Schulen und in Amalner, Mumbai und Pune (alle in Mahararashtra). 1919 wird er in Varanasi (Uttar Pradesh) von Jagadguru Śaṅkarācārya Svāmī Trivikrāma Tīrthains ins Sannyasa eingeführt, der letzten von vier Entwicklungsstufen (Ashramas) des Lebens als Hindu und trägt von nun an den Namen Swami Bharatikrishna Tirtha.
1921 wird eine Fatwa gegen ihn verhängt, er entkommt nur knapp einer Gefängnisstrafe. 1925 wird er der 143. Sankaracarya (spiritueller Führer) im Kloster Dwarka Sharada Math in Dwarka (Gujarat).
In den nächsten 35 Jahren veröffentlicht er zahlreiche Bücher über Religion, Naturwissenschaft, Mathematik, Weltfrieden und soziale Themen, reist um den Globus und fördert die Verbreitung indischer Kultur und des Dharma, die Lehre von den Pflichten des Individuums und der universellen Ordnung.
Er ist der erste Sankaracarya, der andere Länder bereist und seine philosophischen Lehren und mathematischen Konzepte werden heute noch in Indien in Vorträgen und Seminaren weitergegeben. In spirituellen Zentren hält man ihm zu Ehren Veranstaltungen ab. Jagadguru Śaṅkarācārya Svāmī Bhāratīkṛṣṇa Tīrtha stirbt am 2. Februar 1960 in Puri (Odisha), einer bedeutenden Pilgerstadt am Golf von Bengalen.


