Die Kreiszahl π wird auch Archimedes-Konstante und Ludolphsche Zahl genannt. Namensgeber für π ist der erste Buchstabe des griechischen Worts "perímetros" ("Umfang"). Populär machte seine Verwendung Leonhard Euler (1707-1783), der π ab 1737 verwendete. Ihm haben wir auch den größten Konkurrenten um die Spitzenposition als Ikone der Zahlenfreunde zu verdanken, die Eulersche Zahl e. Beide sind transzendent und daher irrational.
Auch wenn die Freude an Zahlentheorie und Mathematik im Allgemeinen von vielen als nicht ganz nachvollziehbar angesehen wird, haben Transzendenz und Irrationalität mathematisch eine andere Bedeutung als im normalen Sprachgebrauch. Werfen wir das Rampenlicht zuerst auf die immer präzisere Berechnung der Kommastellen unseres Superstars, bevor wir uns vorsichtig der Theorie dahinter zuwenden.
Unendliche Stellensuche
Bereits in der babylonischen Mathematik (1900-1600 v.Chr.) verwendete man für π einen Wert von π=3,125. Dazu näherte man sich dem Kreisumfang mit einem entsprechenden Sechseck. Aus der altägyptischen Mathematik ist ein Näherungswert von π=3,16 bekannt (ca.1650 v.Chr.), der anhand der Quadratur des Kreises - also dem Flächenvergleich von Quadrat und Kreis - ermittelt wurde.
Das Alte Testament nennt für π im 1.Buch der Könige 7, Vers 23 (ca. 1000 v.Chr.): "Ein Rundbecken mit einem Durchmesser von 10 Ellen hatte einen Umfang von 30 Ellen.", also für π ≈ 3.0. In Indien wurde in der Baudhayana Sulbasutra (ca. 800 v.Chr.) ein Wert von π ≈ 3.088 angegeben. Auch dort basierte die Berechnung auf für Zeit und Ort typischen geometrischen Konstruktionen.
Der erste, der mathematisch belegte Ober- und Untergrenzen für π angab, war der griechische Erfinder und Mathematiker Archimedes (287-212 v.Chr.). In "Die Kreismessung" ("kýklou métrēsis", 250 v.Chr.) nähert er sich π durch um- und eingeschriebene regelmäßige Vielecke, beginnend beim Sechseck. Durch Verdoppeln erhöht er die Anzahl der Ecken auf 96 und ermittelt damit einen Wert, der zwischen 223/71 und 22/7 liegt. 3,1408450 < π < 3,1428571 reicht aus um zumindest die beiden ersten Kommastellen korrekt anzugeben.
In der Praxis verwendete man einfach das Ergebnis aus 22/7. Eine Abweichung von 0,04% vom genauen Wert war für Konstrukteure und Baumeister anscheinend völlig ausreichend - viele der damit errichteten Bauwerke stehen ja heute noch. Claudius Ptolemäus (100-160) erhöht die Ecken des, dem Kreis umschriebenen, regelmäßigen Vielecks auf 120 und damit weiter die Genauigkeit. Für mehr als zwei korrekte Stellen reicht das aber auch nicht. Im westlichen Kulturkreis sollte sich dann in den nächsten 1700 Jahren niemand mehr finden, der diesen Wert weiter präzisieren konnte.
Um 480 n.Chr. berechnet der chinesische Mathematiker Zu Chongzhi (429-500) π bereits auf 6 Nachkommastellen genau - ein Wert der dann mehr als 900 Jahre nicht mehr übertroffen wurde. Er nutzt die Methode unendlicher Reihen beim Einbeschreiben regelmäßiger Vielecke und findet damit seine "genaue Näherung" ("milu") von 355/113. Für seine Berechnungen verwendet er "Zählstäbchen" ("chóu") - eine Rechenhilfe aus Holz, mit der chinesische Mathematiker Zahlen und Rechenschritte darstellten. Die Seitenanzahl der eingeschriebenen regelmäßigen Vielecke stieg auf 12.288.
In mittelalterlichen Indien beschäftigt sich der Gründer der berühmten Kerala-Schule, Madhava von Sangamagrama (1350-1425) mit der Berechnung der Kreiszahl. Er bestimmt mithilfe einer unendlichen Reihe und der Infinitesimalrechnung ihren Wert mit einer Genauigkeit von 13 Kommastellen.
In Samarkand (im heutigen Usbekistan) berechnet ungefähr zur selben Zeit der islamische Mathematiker Ghiyath ad-Din Dschamschid bin Masʿud bin Muhammad al-Kaschi - oder einfach al-Kaschi (1380-1429) - mit numerischen Methoden den Umfang des Einheitskreises mit einem 3x2²⁸-Eck auf 15 Stellen genau.
Ludolph van Ceulen (1540-1610) verwendet gute 100 Jahre später ebenfalls die klassische Annäherung über umschriebene Vielecke und erhöht nach diesem Prinzip die Anzahl der Ecken auf 2⁶². Damit kommt er nach 30 Jahren Rechenarbeit auf 35 Stellen hinterm Komma.
Effizienter als die Methode des klassischen Um- und Einschreibens ist die Verwendung der Reihenentwicklung des Arctangens. So kommt John Machin (1680-1751) auf 100 Stellen. William Shanks (1812-1882) errechnet in Jahrzehnte langer Arbeit 707 Dezimalstellen. Ein kleiner Rechenfehler - der erst 1946 entdeckt wird - sorgt dafür, dass "nur" die ersten 527 Stellen davon korrekt sind.
Shanks 527 Stellen bleiben bis zum Aufkommen der ersten Computer mit Elektronenröhren (genaueres dazu hier) in den 40er Jahren des letzten Jahrhunderts unerreicht. In der Zeit dazwischen werden zwar Methoden und Algorithmen verbessert, die führen aber erst mit der Ausführung durch elektronische Rechner zu höherer Genauigkeit.
1949 bricht der mit 17.468 Röhren bestückte amerikanische ENIAC nach 70 Stunden Rechenarbeit und einem Stromkonsum von rund 10.000 Kilowattstunden den Rekord von Shank: 2.037 Stellen hinterm Komma, ablesbar an den gut 50.000 Löchern in den bis zu tausend verwendeten Lochkarten für die analoge Ausgabe.
Die weitere Erhöhung der Nachkommastellen von π verläuft bis heute parallel zur Evolution der elektronischen Rechenknechte und ihrer Algorithmen. Der IBM 7090 ist nach 8 Stunden Rechenzeit mit 100.265 Stellen Rekordhalter im Jahr 1961. Cray-Rechner in den 80ern erhöhen den Wert auf einige Millionen Stellen.
Mit einer 1988 von den Brüdern David und Gregory Chudnovsky veröffentlichten Formel und dem Einsatz von Hitachi-Supercomputern kommt der japanische Informatiker Yasumasa Kanada 1995 auf 4,29 Milliarden, 1999 auf 206 Milliarden und 2002 auf 1,2 Billionen Stellen. Dafür schluckt der damals als ressourcenschonend bekannte Hitachi SR8000/MPP satte 192.000 Kilowattstunden in den 600 Stunden Rechenzeit.
Was der Stromzähler der Google Cloud 2022 für 157 Tage Rechenzeit und den neuen Rekord von 100 Billionen Stellen anzeigte? 5-6 Millionen Kilowattstunden. Was für ein Glück, dass die alle durch Emissionszertifikat-Handel zu 100% erneuerbar sind. Mein mit künstlicher Intelligenz ausgestatteter Assistent möchte mir diesen explosionsartig ansteigenden Energiebedarf (Jahresstrombedarf von 1500 Erste-Welt-Haushalten für eine einzige Berechnung) sogar als "geringeren ökologischen Fußabdruck als bei den Berechnungen davor" verkaufen - netter Versuch, TechnoSoph lacht darüber genauso gern wie die Betreiber von Kernkraftwerken.
Für das Jahr 2025 meldet das "Guiness Buch der Rekorde" für die Zahl π 300 Billionen Stellen hinterm Komma (die 300-billionste ist übrigens 5) - aufgestellt durch die Linus Media Group & Kioxia in mehr als 7 Monaten Rechenzeit auf einem lokalen, NAS-gebundenen System mit 2,2 Petabyte Speicher, 3 Terabyte RAM und einem einzigen Prozessor: AMD EPYC 9684X mit 96 Kernen und 192 Threads. Stromverbrauch in den 7 Monaten: nur ein Fünfhundertstel der Cloud-Lösung von Google.
Die Effizienzsteigerung resultiert aus der Integration des AMD EPYC zusammen mit unfassbar viel RAM im Vergleich zu den unzähligen verteilten Servern in der Google Cloud. Lokale Optimierung und ein weiterentwickelter Chudnovsky-Algorithmus sind weitere Gründe für die immense Ressourcenschonung im Vergleich zum vorherigen Rekordhalter.
Die Suche nach immer weiteren unentdeckten Kommastellen von π liefert hauptsächlich brauchbare Erkenntnisse für Ingenieure und Softwareentwickler, der praktische Nutzen für die Zahlentheorie hält sich in Grenzen. Interessanter wären (mit KI entdeckte?) Beweise für noch unbekannte Eigenschaften der Kreiszahl, aber lassen wir uns überraschen.
Von der Geometrie zur Analysis
Maximal ressourcenschonend ist der Einsatz von Zirkel und Lineal: Archimedes benutzte - bevor seine Kreise 212 v.Chr. von einem römischen Soldaten ein letztes Mal gestört wurden - wie bereits erwähnt einerseits Vielecke mit bis zu 96 Ecken, die er in den Kreis eingeschrieben oder sie damit umschrieben hat. Definition von π durch die Proportionalität von Umfang und Durchmesser ist
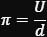
Als zweite geometrische Methode kam die Berechnung des Verhältnisses des Flächeninhalts eines Kreises zum Flächeninhalt des ihn umschreibenden Quadrats zum Einsatz. Ein Kreis mit Radius r besitzt die Fläche π·r², während das ihn umschreibende Quadrat die Fläche 4·r² besitzt. Daraus ergibt sich ein Verhältnis von π : 4. Dieses Verhältnis zeigt, wie viel Fläche ein Kreis im Vergleich zum ihn umgebenden Quadrat einnimmt – und ist zugleich eine geometrische Veranschaulichung der Zahl π.
Zu Chongzhi führte mit Grenzwertbetrachtungen und Interpolationstechniken die geometrischen Methoden von Archimedes und Ptolemäus in eine algorithmische Frühform der Analysis. Sein Werk "Methoden der Interpolation" ("Zhui Shu") ging leider verloren, aber es wird vermutet, dass es frühe Formen von Reihen und Integrationsmethoden enthielt. Den Wert von 355/113 für 6 korrekte Kommastellen fand er vermutlich durch Bruchinterpolation der Werte zwischen 22/7 und 3/1 mit den Schranken aus 3,1415926 < π < 3,1415927 - Werte, die sich anhand seines 12.288-seitigen regelmäßigen, dem Kreis umschriebenen, Polygons ergaben.
Leider sind auch die Originalschriften von Madhava nicht mehr erhalten, seine Methoden lassen sich aber aus späteren Werken wie dem "Tantrasangraha" und dem "Yuktibhāṣā" (um 1530) rekonstruieren. Demnach fand er (250 Jahre vor Leibniz) mit einer Kombination aus geometrischer Intuition, trigonometrischer Analyse und astronomischer Praxis die unendliche, heute auch nach ihm benannte Madhava-Leibniz-Reihe:
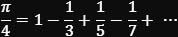
Sie ist die Potenzreihe der arctan(1)-Funktion, also der Umkehrfunktion einer geeignet eingeschränkten Tangensfunktion.
Setzt man x=1, erhält man arctan(1)=π/4
Im Rahmen astronomischer Modelle analysierte er Kreisbewegungen und Winkel und erkannte, dass sich der Bogen eines Kreises durch eine Reihe von geraden und ungeraden Näherungstermen ausdrücken lässt. Vermutlich durch geometrische Zerlegung des Kreisbogens entstandene Abschnitte approximierte er mit algebraischen Ausdrücken und führte zugleich Korrekturterme wie
ein.
Diese waren notwendig, da die Madhava-Leibniz-Reihe logarithmisch langsam konvergiert - man also ziemlich viele Rechenschritte benötigt um ein genaueres Ergebnis zu erhalten. Ohne Korrekturterme sind für 3 korrekte Dezimalstellen von π rund 5.000 Terme nötig, für 5 aber bereits eine Million.
Madhavas Arbeiten blieben im Westen über Jahrhunderte unbekannt und waren ihrer Zeit weit voraus. Sie gelten heute als lange unsichtbarer Wegweiser in die moderne Mathematik. Im Westen sichtbar war hingegen die Arbeit von James Gregory, einem schottischen Mathematiker (1638-1675), der 1671 dieselbe Reihe entwickelte wie Madhava - aus der Integraldarstellung von arctan(x) und ohne Kenntnis von Madhavas Arbeiten. Die moderne Bezeichnung lautet daher oft auch Madhava–Gregory–Leibniz-Reihe. Leibniz entdeckte sie zwischen 1673 und 1676 ebenfalls aus der Ableitung von F(x)=arctan(x) und sorgte für ihre weitere Verbreitung.
diese Funktion ist die Ableitung von
daraus ergibt sich
Leibniz entwickelte den zu integrierenden Term als Potenzreihe
und durch Integration dieser Reihe von 0 bis 1 erhielt er ebenfalls:
John Machins entwickelte daraus eine weitere Arctan-Reihe mit schnellerer Konvergenz:
Bereits 1593 fand der französische Mathematiker und Jurist François Viète (1540–1603), ausgehend von den Flächen- und Umfangverhältnissen dem Kreis eingeschriebener Polygone, eine Darstellung für 2/π als unendliches Produkt, bei dem jede Wurzel tiefer geschachtelt ist als die vorige. Es konvergiert gegen 2/π, sodass man durch Umkehrung π erhält:
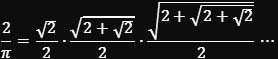
Viètes Formel war die erste bekannte unendliche Produktdarstellung in der europäischen Mathematik und markiert den Beginn der mathematischen Analysis in Europa. Seine 9 korrekten Nachkommastellen von π reichen nur für den damaligen Europarekord, daher fehlt er im historischen Teil weiter oben.
Heute wird ein Äquivalent zu seiner Formel durch trigonometrische Identitäten hergeleitet:
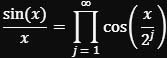
setzt man x=π/2, ergibt sich:
Von der Statistik zur Chaostheorie
Einen verblüffenden, Wahrscheinlichkeiten nutzenden, experimentellen Ansatz zur Berechnung von π fand der französische Naturforscher Georges-Louis Leclerc, Comte de Buffon (1707-1788). Seine Idee war, Nadeln zufällig auf einen Boden mit parallelen Linien zu werfen und damit den Wert für π zu berechnen.
Aus geometrischen Überlegungen ging Buffon davon aus, dass die Wahrscheinlichkeit mit der eine Nadel eine Linie schneidet, von drei Faktoren abhängt: der Länge der Nadel, dem Abstand der Linien und dem Winkel, in dem die Nadel fällt. Bei bestimmten Längenverhältnissen sollte sich π daher aus der Trefferwahrscheinlichkeit ablesen lassen.
1733 stellte er seine auf Geometrie und Statistik beruhende Methode der Akademie der Wissenschaften in Paris vor. Sie erhielt begeisterte Gutachten, wurde jedoch lange unterschätzt, weil sie auf Zufall und Beobachtung statt rein auf Formeln beruhte.
Formel für das Buffon'sche Nadelproblem - π bekommt das in der Statistik übliche Hütchen (Zirkumflex) als Zeichen der Approximation:
l: Länge der Nadel
d: Abstand zwischen den Linien
N: Gesamtzahl der geworfenen Nadeln
C: Anzahl der Nadeln, die eine Linie schneiden
Im Spezialfall mit Nadeln, die kürzer sind als der Linienabstand, vereinfacht sich die Formel für die Trefferwahrscheinlichkeit:
dabei ist
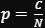
die relative Häufigkeit der Treffer.
Wirft man 1000 Nadeln der Länge l=2cm auf Linien mit dem Abstand d=3cm, sollten im Mittel 636 davon die Linien treffen. Das kann ja jeder gerne zuhause selbst probieren. Daraus ergibt sich
Mit der algorithmische Weiterentwicklung dieses Ansatzes ab den 1940ern durch Ulam, von Neumann, Fermi u.a. lässt sich nicht nur π besser berechnen. Die sogenannte Monte-Carlo-Methode wurde eigentlich für die Simulation von Neutronenbewegungen im Manhattan-Projekt entwickelt und findet heute Anwendung in verschiedensten Gebieten - vom maschinellen Lernen bis zur Kursanalyse an den Börsen.
Dazu landen keine Nadeln auf Linien, aber (simulierte) zufällige Punkte innerhalb eines Quadrats mit eingeschriebenem Einheitskreis. Verhältnis der Treffer im Kreis zu den Gesamtpunkten ≈ π/4.
Die erste Formel, die ein Computer für die Berechnung von π fand, ist die Bailey–Borwein–Plouffe-Formel (BBP) von 1995. Besonders bemerkenswert ist die Möglichkeit, mit ihrer Hilfe beliebige Stellen von π im Hexadezimalsystem (Basis 16) zu berechnen, ohne die vorherigen Stellen zu kennen.
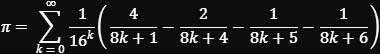
Die heute bevorzugte Methode zur Berechnung von Billionen Stellen von π basiert auf einer hypergeometrischen Reihe, die extrem schnell konvergiert. Die Rekorde von Yasumasa Kanada über Google bis zur Linus Media Group beruhen auf - für die jeweilige Hardware optimierten - Programmen, die einen Algorithmus der Brüder Chudnovsky nutzen. Die nicht besonders hübsche Formel
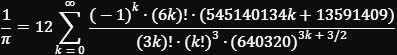
liefert bei jeder Iteration etwa 14,18 Dezimalstellen von π und basiert im Kern auf einer Formel des indischen Mathematikers Srinivasa Ramanujan (1887–1920) für 1/π:
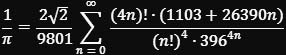
Ramanujans Formeln erzeugen Ziffern von π, die statistisch zufällig erscheinen, obwohl sie deterministisch berechnet werden. Er nahm damit Konzepte wie Normalität, Zufallsverteilung und komplexe Muster – zentrale Themen der Chaostheorie - vorweg. Ein Zusammenhang von Ordnung und Zufall, der auch in der Arbeit von Bailey, Borwein und Plouffe auftaucht, das aber erst rund 80 Jahre später.
Die Art und Weise, wie Ramanujan seine Berechnungen erstellte, war mehr als unorthodox und wird hier nicht weiter angerissen. Ihm und seinen unglaublichen Entdeckungen ist ein eigener Artikel auf Technosoph|Mathematik gewidmet: "Srinivasa Ramanujan - im Kosmos der Zahlen".
Eigenschaften
π ist nicht nur eine geometrische Konstante, die sich aus dem Verhältnis eines Kreises zu seinem Umfang ergibt, sie ist auch ein statistisches Phänomen. Obwohl sie deterministisch berechnet werden kann, wirkt sie chaotisch - es gibt in ihr kein Muster oder Wiederholung und das endlos. Jede neue Stelle scheint stets neu gewürfelt.
π ist also eine unendliche, nicht periodische Dezimalzahl, von der man vermutet, dass sie eine normale Zahl ist. Kennzeichen einer normalen Zahl ist die gleichmäßige Verteilung aller Ziffern (0-9) in der Dezimaldarstellung. Beweis dafür gibt es bisher keinen, aber diese Vermutung wird inzwischen durch Billionen berechneter Kommastellen experimentell unterstützt.
π ist irrational: es kann nicht als Bruch zweier ganzer Zahlen dargestellt werden. Den Beweis für seine Irrationalität erbrachte 1761 Johann Heinrich Lambert (1728-1777):
1. Ist x rational (und ungleich null), dann ist tan(x) irrational.
2. Er bewies dies mit einer Kettenbruchdarstellung für den Tangens.
3. Da tan(π/4) =1 und 1 ist rational, folgt: π/4 kann nicht rational sein, also ist π irrational.
Lamberts Kettenbruchdarstellung:
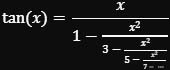
π ist transzendent: es ist keine Lösung irgendeines algebraischen Polynoms mit ganzzahligen Koeffizienten. Ferdinand von Lindemann (1852-1939) erbrachte 1882 den Beweis für die Transzendenz von π. Dieser Beweis lieferte das erste echte mathematische Argument dafür, dass die Quadratur des Kreises mit Zirkel und Lineal unmöglich ist.
Dazu verallgemeinerte er den Transzendenzbeweises für e durch Charles Hermite (1822-1901), was zum Lindemann–Weierstraß-Satz führte. Zentrale Aussage: wenn 
algebraische Zahlen sind, die paarweise verschieden und nicht null, dann sind die Zahlen 
linear unabhängig über den algebraischen Zahlen.
Seine Beweisidee für die Transzendenz von π lautete:
1.Annahme: π sei algebraisch.
2.Dann ist auch i·π algebraisch, da i selbst algebraisch ist.
3.Nach dem Lindemann–Weierstraß-Satz wäre dann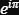 
transzendent.
4.
und -1 ist algebraisch
5.Widerspruch: kann nicht gleichzeitig transzendent und algebraisch sein.
6.Folgerung: π kann nicht algebraisch sein, daher ist π transzendent.
Obwohl π transzendent ist, gehört es zur Klasse der Perioden im Sinne von Kontsevich und Zagier. Perioden sind komplexe Zahlen, die sich als Integrale von rationalen Funktionen über algebraische Mengen darstellen lassen.
Pi-raten und schweigsame Aliens
Die Kreiszahl π beschäftigt seit Jahrtausenden Mathematiker. Sie ist eine der fundamentalsten Konstanten der Mathematik und wurde im Lauf der Zeit auch zu einem Phänomen der Popkultur und zu einer Ikone der Zahlenfreunde.
Dass ausgerechnet der 14.März zum Pi-Tag erklärt wurde, überrascht nicht, wenn man das US-Datumsformat im Kalender nutzt - so wie sein Begründer, der amerikanische Physiker Larry Shaw. Seit 1988 begeht man diesen Tag am Exploratorium in San Francisco.
2009 erklärte der US-Kongress den 14. März offiziell zum National Pi Day und seit 2020 gibt es den Internationale Tag der Mathematik, ausgerufen von der UNESCO. Albert Einsteins Geburtstag am 14.März ist allerdings reiner Zufall.
Die deutsche Piratenpartei wählte die Pi -Ratte als Maskottchen. Niemand weiß, ob diese Pi-Rat der Partei bisher beim Erreichen der politischen Quadratur des Kreises behilflich oder eher hinderlich war.
Den Rekord im Auswendiglernen der Kommastellen von Pi hält zurzeit Rajveer Meena aus Indien - mit 70.000 Nachkommastellen.
Der Senat des US-amerikanischen Bundesstaats Indiana machte es sich besonders leicht und legte in einem Gesetzesentwurf 1897 den Wert für Pi einfach per Verordnung mit 4 fest. Aus dem mathematischen Unsinn und dem inhaltlich verworrenen Gesetz wurde auch mit einem Wert von 3,2 nichts - das Gesetz trat nie in Kraft.
Da im (vermutlich) isotropen Universum das Verhältnis von Durchmesser zum Kreisumfang überall dasselbe sein sollte, wurde Pi auch Teil der Botschaft im Rahmen intergalaktischer Kontaktaufnahme durch Projekte wie der noch laufenden SETI-Initiative, der Arecibo-Botschaft (1974) oder von Cosmic Call (1999-2003).
Auf Antworten wird noch gewartet, wahrscheinlich sind die Außerirdischen noch mit der Berechnung weiterer Nachkommastellen beschäftigt und hatten daher noch keine Zeit zurück zu funken. Das verschafft uns noch etwas Zeit um mit Nachdruck unsere irdischen Methoden zur Berechnung von Pi weiter zu optimieren und schnell noch ein paar neue Stellen hinterm Komma aufzudecken - damit wir uns vor unseren Freunden in den fliegenden Untertassen nicht völlig blamieren, wenn sie wieder mal bei uns nach dem Rechten schauen...